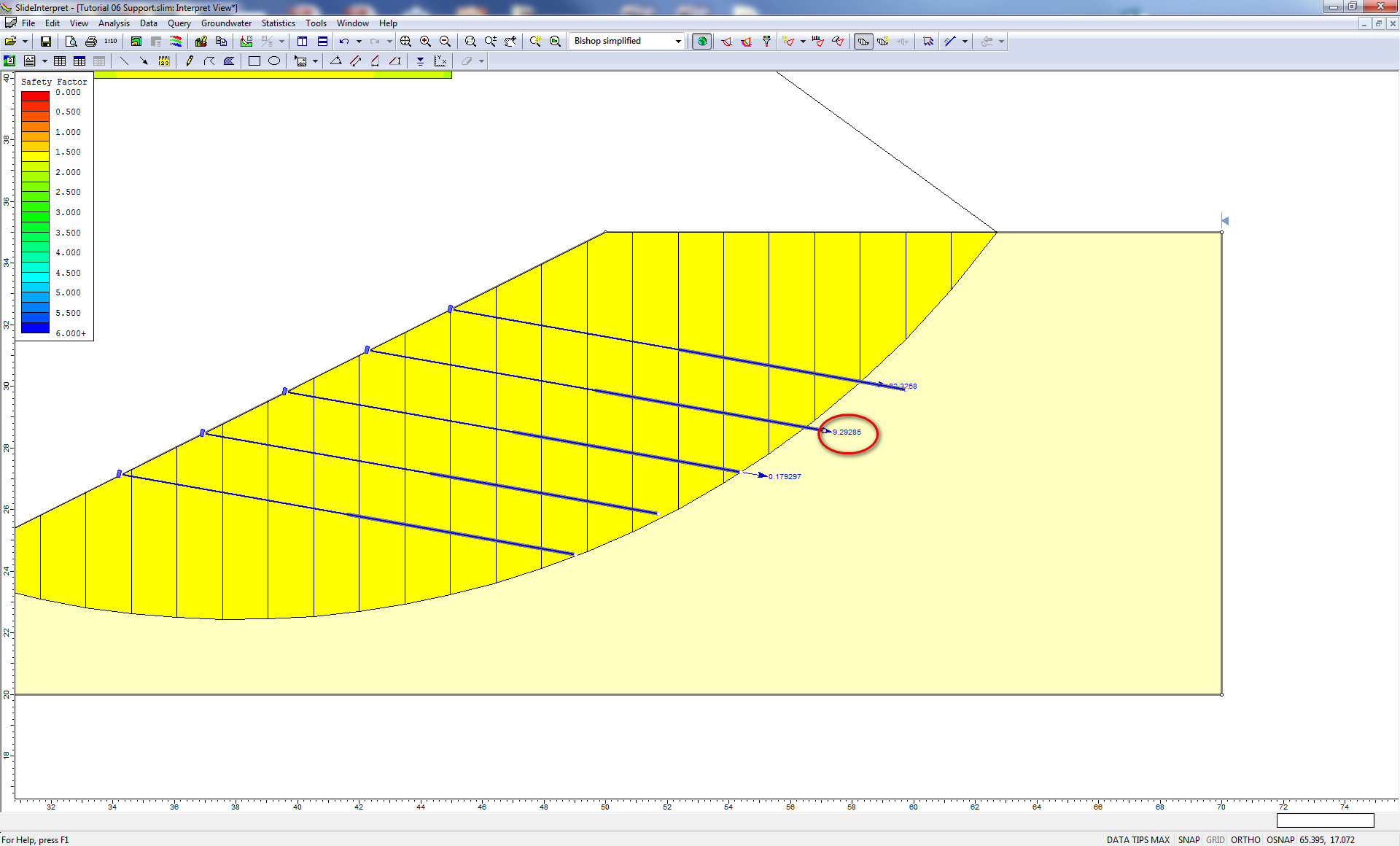
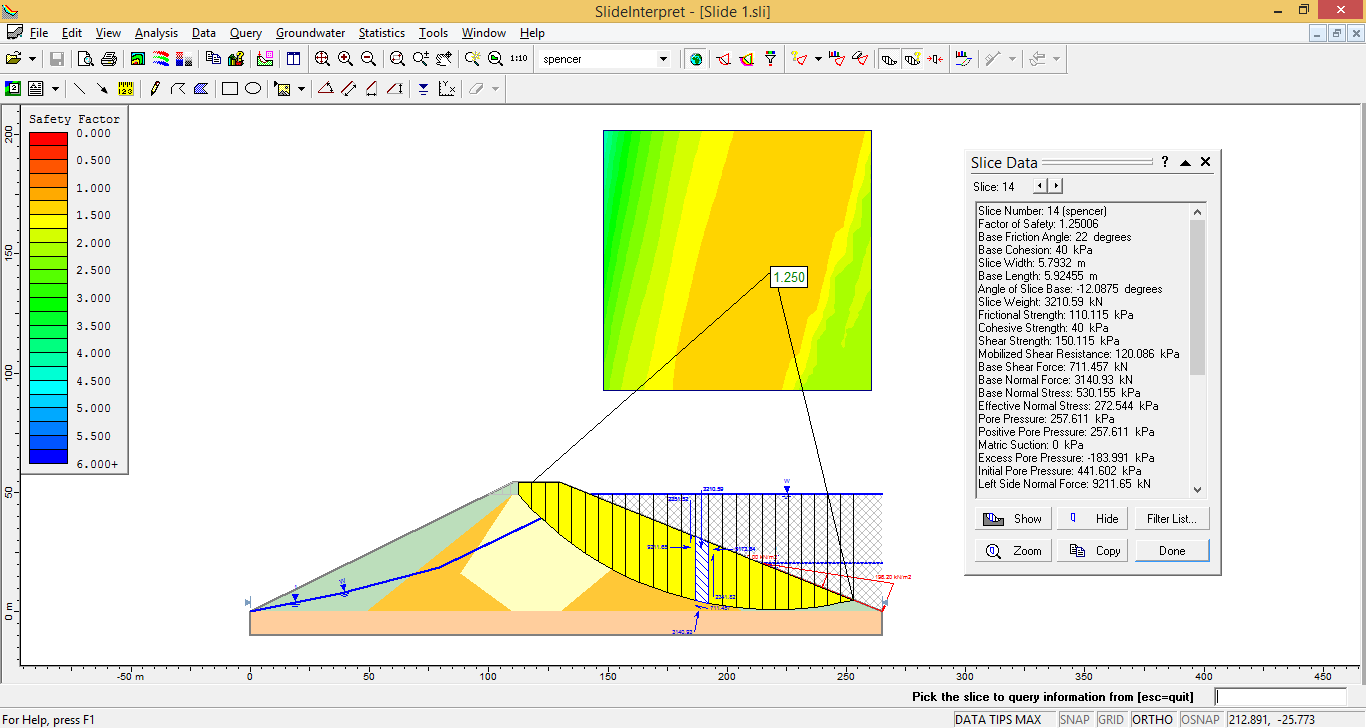
La teoría de estabilidad de taludes se basa en los conceptos básicos de “Empuje de Tierra Lateral”, el cual trata de la magnitud y distribución del empuje lateral entre una masa de suelo, y la estructura de tierra de retención adyacente.
Las dos teorías clásicas de empuje de tierra son las debidas a Coulomb (1776) y a Rankine (1857). La teoría de Rankine considera los esfuerzos en una masa de suelo cuando alcanza un estado de equilibrio plástico, es decir, cuando se está por alcanzar el punto de rotura por corte en la masa de suelo.
A partir de esto se definió que la masa de suelo en estado de equilibrio estático; posee una deformación unitaria horizontal de 0. La relación del esfuerzo efectivo horizontal respecto del esfuerzo vertical se llama coeficiente de presión de tierra en reposo, Ko.
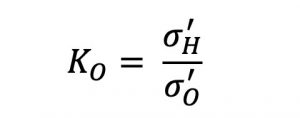
Para suelos de grano grueso, el coeficiente de presión de tierra en reposo se estima por la relación empírica de Jaky (1944).
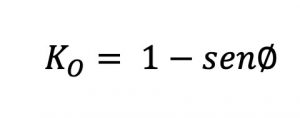
TEORÍA DE RANKINE ACTIVA Y PASIVA
El término equilibrio plástico en suelos se refiere a la condición en que cada punto en una masa de suelo está a punto de fallar. Rankine (1857) investigó las condiciones de esfuerzo en el suelo en un estado de equilibrio plástico.
Realizando las ecuaciones sobre la cuña, se tiene la razón de s’a respecto a s’o se llama coeficiente de presión de tierra activa de Rankine, Ka.
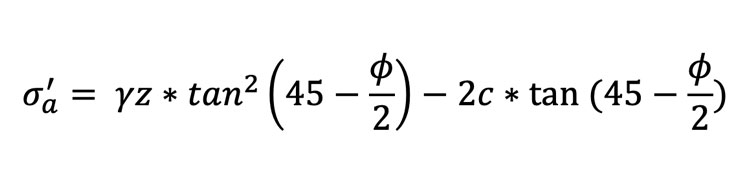
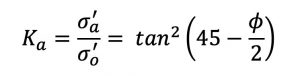
Dicho coeficiente de presión activa puede ser escrito también de la siguiente forma:
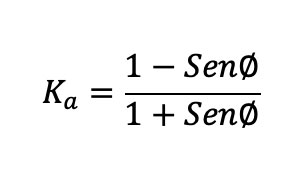
El esfuerzo horizontal se define como la presión activa (pa), debida indirectamente al peso propio del suelo.
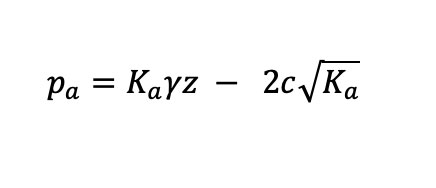
De otro lado, el estado pasivo de Rankine muestra la variación de la presión pasiva con la profundidad. Para suelos sin cohesión (c = 0)
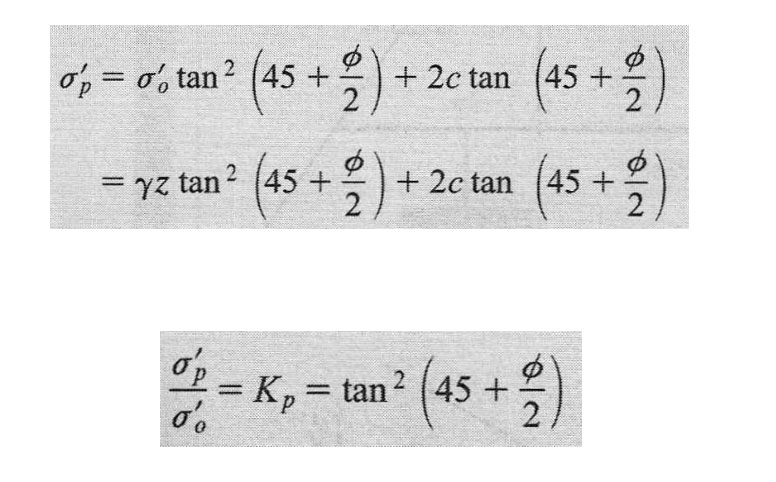
Kp se denomina coeficiente de presión de tierra pasiva de Rankine.
Se sabe que se alcanza el valor máximo s1, cuando el círculo de Mohr que pasa por el punto que representa el valor fijo s3, toca la envolvente de rotura del suelo. En ese caso se define al esfuerzo horizontal como la presión pasiva (pp), que representa la resistencia inherente máxima del suelo, a la comprensión lateral.
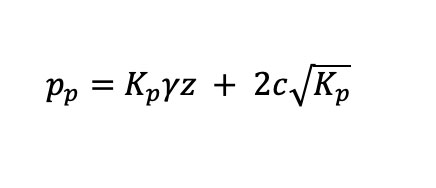
Las presiones activa y pasiva aumentan linealmente con la profundidad. Cuando c = 0, en cada caso se obtienen distribuciones triangulares.
Cuando c es mayor que cero, el valor de pa es cero a una profundidad determinada zo. Se tiene entonces con pa = 0
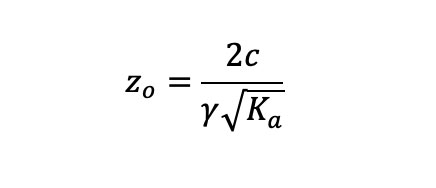
A la fuerza por unidad de longitud de pared, debida a la distribución de presión activa, se la denomina EMPUJE ACTIVO TOTAL (PA), para una pared vertical de altura H:
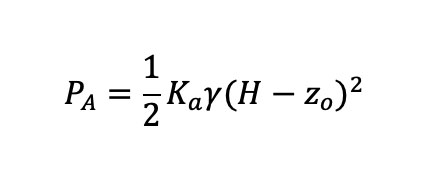
A la fuerza debida a la distribución de presión pasiva se la denomina RESISTENCIA TOTAL PASIVA (PP). Para una superficie de pared vertical de altura H:
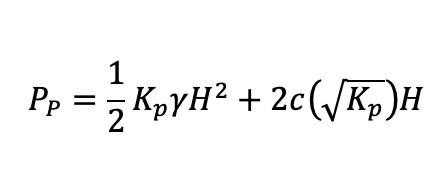
Todas estas expresiones cambian si el suelo se haya por debajo de la tabla de agua, bajo condición totalmente drenada, las presiones activa y pasiva deben ser expresadas en términos del peso efectivo del suelo, y los parámetros de esfuerzo efectivo c’ y f’.
También se puede aplicar la teoría de Rankine a casos en que la superficie del suelo presenta una inclinación de ángulo constante β, respecto a la horizontal. Se supone que las presiones activa y pasiva, actúan en una dirección paralela a la de la superficie en pendiente.
El coeficiente de presión activa se transforma en:
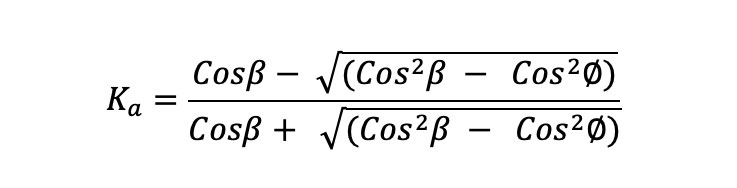
Entonces la presión activa, actuando paralelamente a la pendiente, está dada por:
pa=Ka γzCosβ
y el empuje total activo en una pared de superficie vertical de altura H, es:
PA= (1/2) Ka γH2 Cosβ
Entonces la presión pasiva pp, cuando c = 0, el coeficiente de presión pasiva (igual a pp/sz) está dado por:
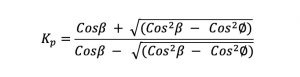
Entonces la presión pasiva, actuando en paralelo con la pendiente, está dada por:
Pp=KpγzCosβ
Y la resistencia pasiva total, en una superficie de pared vertical de altura H, es:
Pp= (1/2) Kp γH2 Cosβ
De las teorías de Rankine y Coulomb se puede llevar dichas ecuaciones para diseñar estructuras de estabilización de taludes, determinando los planos de falla que se producen.
Así, las fuerzas gravitacionales y de filtración tienden a producir una inestabilidad en los taludes naturales formados por excavación, taludes de terraplén y embalses de tierra. Los tipos más importantes de rotura son la circular, no circular, deslizamiento traslacional y deslizamiento compuesto.
En deslizamientos rotacionales, la forma de la superficie circular se halla asociada a condiciones de suelo homogéneas, y los deslizamientos no circulares a condiciones de no homogeneidad. Los deslizamientos traslacionales se dan cuando el estrato adyacente está a una profundidad relativamente pequeña bajo la superficie del talud. La superficie de rotura tiende a ser plana y aproximadamente paralela al talud. Los deslizamientos compuestos tienen lugar generalmente cuando el estrato adyacente está a una profundidad mayor, consistiendo la superficie de rotura en secciones planas y curvas.
En la práctica, se usan métodos de equilibrios límites en el análisis de la estabilidad del talud. Se considera que la rotura está en el punto de ocurrencia a lo largo de una superficie de rotura supuesta o conocida. Se compara la resistencia al corte necesaria para mantener una condición de equilibrio límite con la resistencia al corte disponible en el suelo, dando el factor promedio de seguridad a lo largo de la superficie de rotura. Se considera al problema en 2D, suponiéndose condiciones de deformación plana. Se ha demostrado que un análisis bidimensional da un resultado conservativo para una rotura en una superficie tridimensional (de forma cóncava).
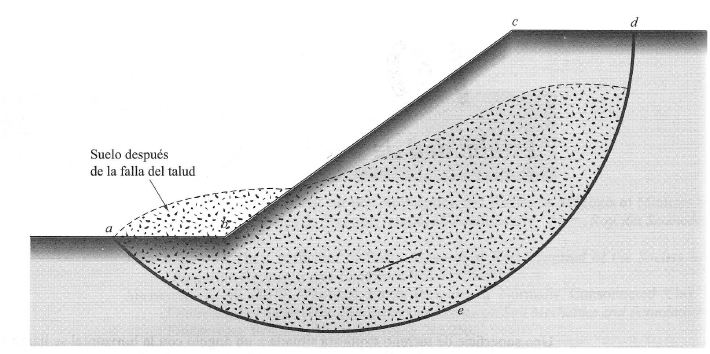
Diferentes métodos de cálculo se pueden emplear para determinar los planos de rotura y estimar los factores de seguridad al deslizamiento (FS).
El método del círculo f
Está expresado en función del esfuerzo total. Se elige una superficie de rotura tentativa un arco circular.
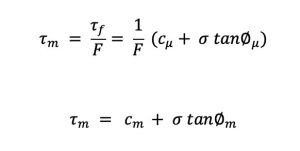
F = factor de seguridad respecto a la resistencia al corte.
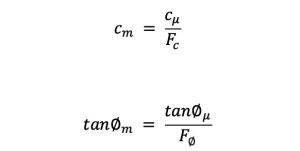
El método de las dovelas
En este método, nuevamente se supone que la superficie potencial de rotura, en sección, es un arco circular de centro O.
Se define al factor de seguridad como la relación entre la resistencia al corte disponible (τf), respecto a la resistencia al corte (τm) que hay que movilizar para mantener una condición de equilibrio límite, es decir:
F = τf / τm
La solución de Fellenius
Esta solución supone que para cada dovela, las fuerzas inter-dovela son cero. La solución involucra la resolución de fuerzas a cada dovela normal a la base, es decir:
N’= WCosα – μl
Por lo tanto, el factor de seguridad en función del esfuerzo efectivo está dado por:
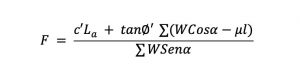
En esfuerzos totales se usan los parámetros cu y fu y el valor de u será igual a cero. El factor de seguridad está dado por:
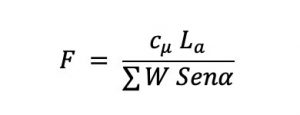
la superficie de rotura potencial se halla parcialmente sumergida y corre paralela a la superficie del talud y está a una profundidad que es pequeña comparada con la longitud del talud.
Ignorando los efectos de los extremos, el talud inclinado en un ángulo β respecto a la horizontal, y la profundidad del plano de rotura z, se toma la tabla de agua como paralela al talud, a una altura mz (0 < m < 1) sobre el plano de rotura.
Finalmente se supone que tiene lugar una infiltración en dirección paralela al talud, y las fuerzas a los lados de cualquier dovela vertical son iguales y opuestas. A su vez, las condiciones de esfuerzo son las mismas en todo punto del plano de rotura.
τf= c’+(σ-μ) tan∅’
y el factor de seguridad es:
F = τf / τ
Las expresiones para s, t y µ son las siguientes:
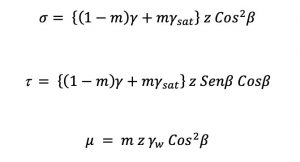
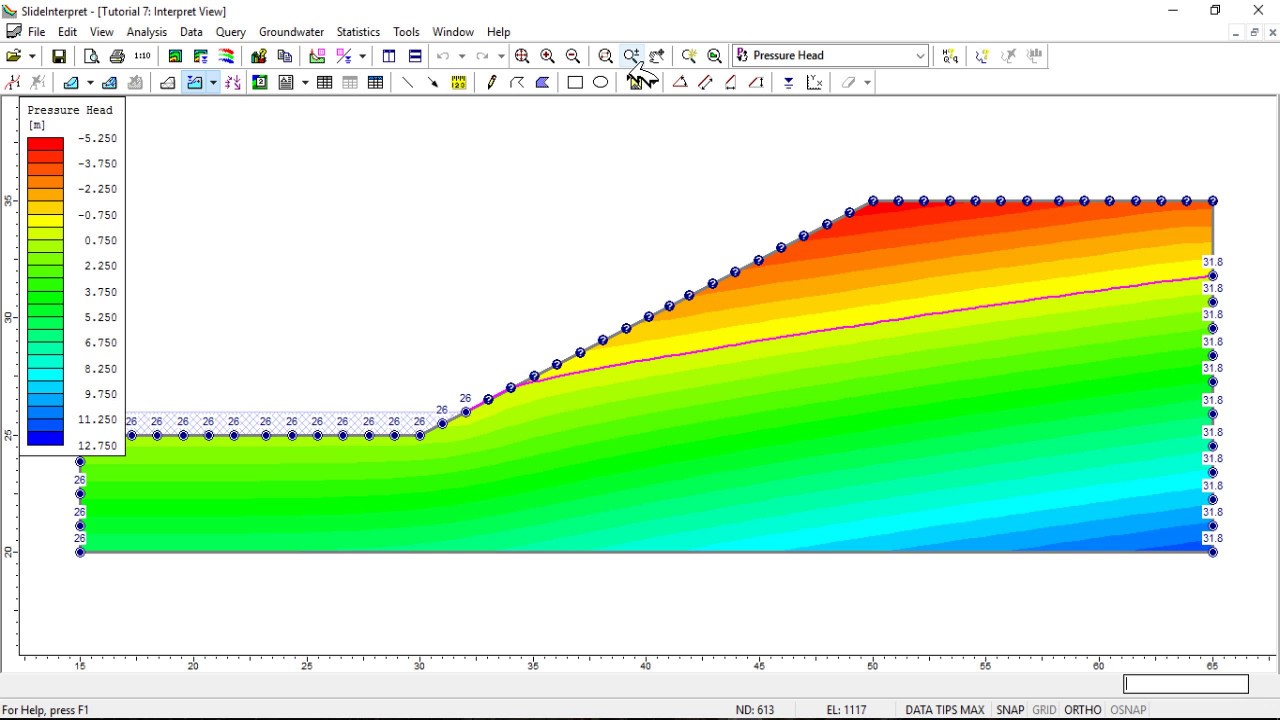
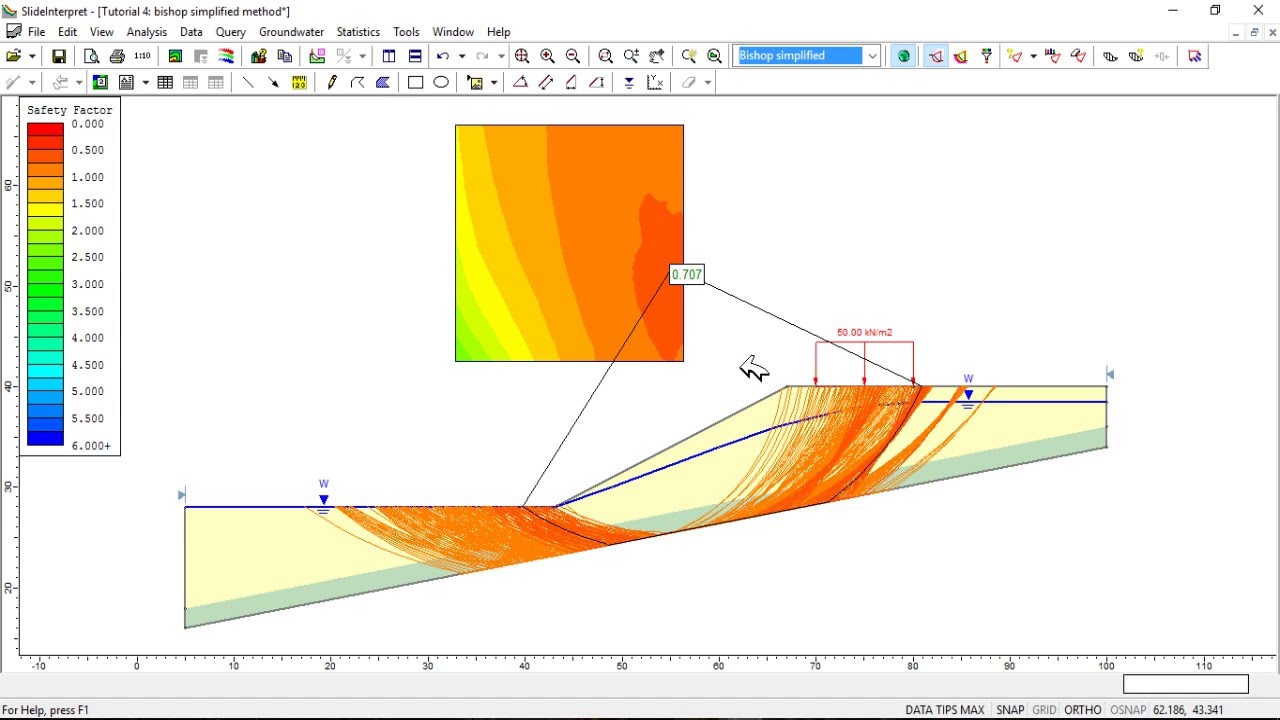
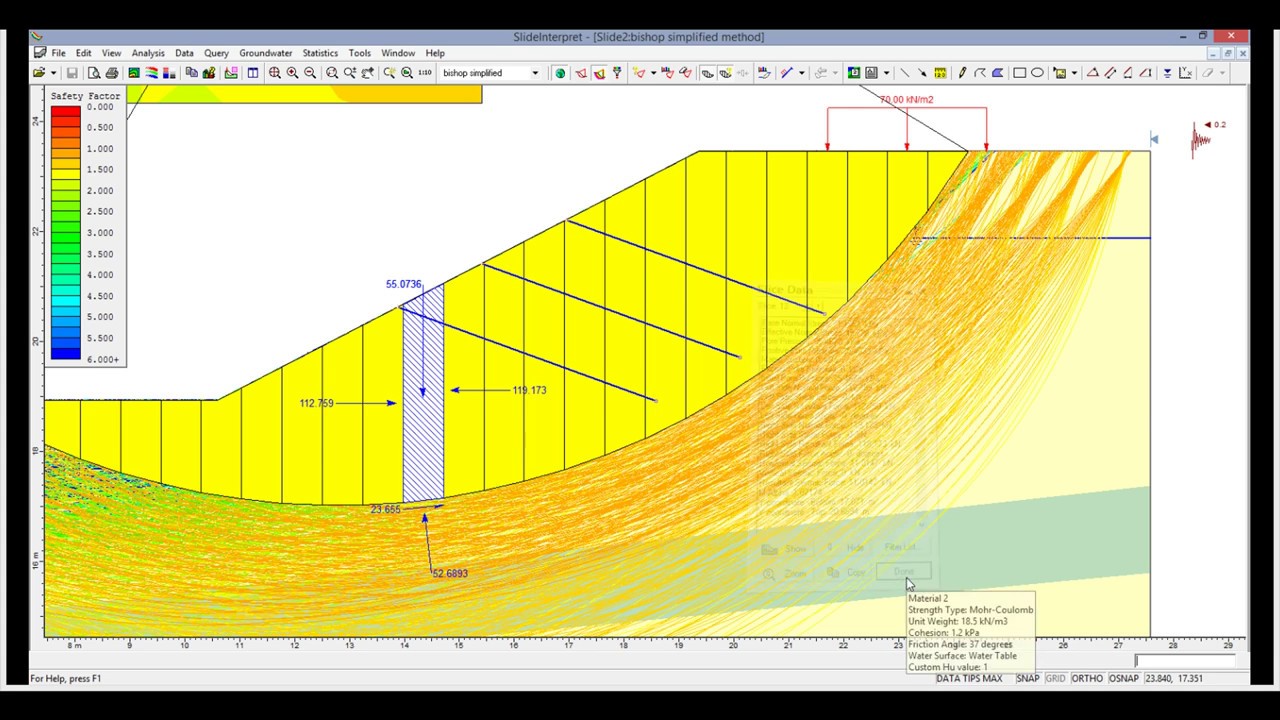
Todos los diseños hasta aquí propuestos serán elaborados mediante programas de cómputo especializados como Rocscience Slide 6.0